Hello, and welcome back to MPC! Last week, we discussed the concept of spacetime and the role it plays in our lives. Today, we will be looking at spacetime a little more closely by analyzing a quantity known as the spacetime interval.
In last week’s post, we discussed how space and time are relative quantities. In other words, the meaning of space (e.g. 1 meter) and time (e.g. 1 second) are different for different people/observers. How so? Using what we have learned about special relativity, we know that time is dilated for some observers and length is contracted for other observers. Therefore, space and time do not have an absolute meaning: if I were to tell you that it took Albert 5 hours to drive to a city that is 300 miles away, a reasonable question would be “relative to whom were these measurements made?” We typically consider space and time to be the most fundamental features of our world, but the fact that they are relative quantities makes them seem a little less “meaningful.”
As we also discussed last week, spacetime is more fundamental than space and time. We also briefly discussed that spacetime provides an absolute quantity, describing space and time, on which everyone will agree (regardless of their motion). Today, we will derive this quantity, known as the spacetime interval.
Let’s think back to the bouncing particle of light we described when we were discussing time dilation. Recall that we had a particle of light starting at the bottom of a rocket ship and had that particle of light move upwards towards the top of the rocket ship. To learn more about the spacetime interval, we will use a similar contraption. This time, however, the particle of light will not be in a moving rocket ship — rather it will be in a box (with a piece of glass as its front) of height h that is “stationary” in outer space:

Figure 1: The bouncing particle of light
**Note: The speed at which the particle moves towards the top of the box is the speed of light, c.**
Now, let’s imagine that we have a rocket ship zooming past the box in Figure 1. We’ll say that this rocket ship is traveling at a certain speed, va, and contains a person, person a:
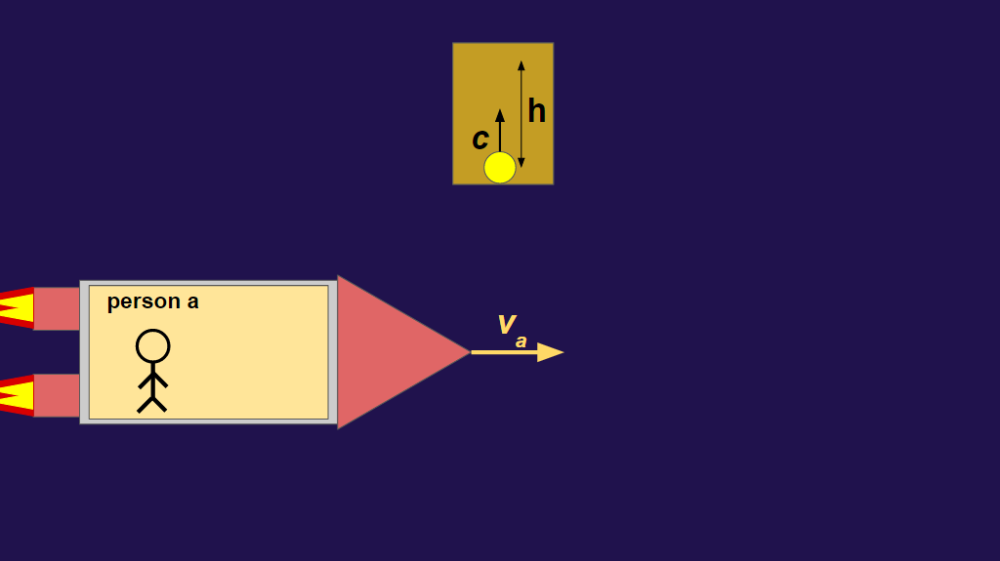
Figure 2: Person a traveling past the box
As person a travels past the box, he will think that the box is traveling past him. To elaborate, person a will see the box approaching/passing him at a speed of va. This is important, for it means that, although the particle of light is only traveling vertically inside of the box, person a will see it traveling diagonally:
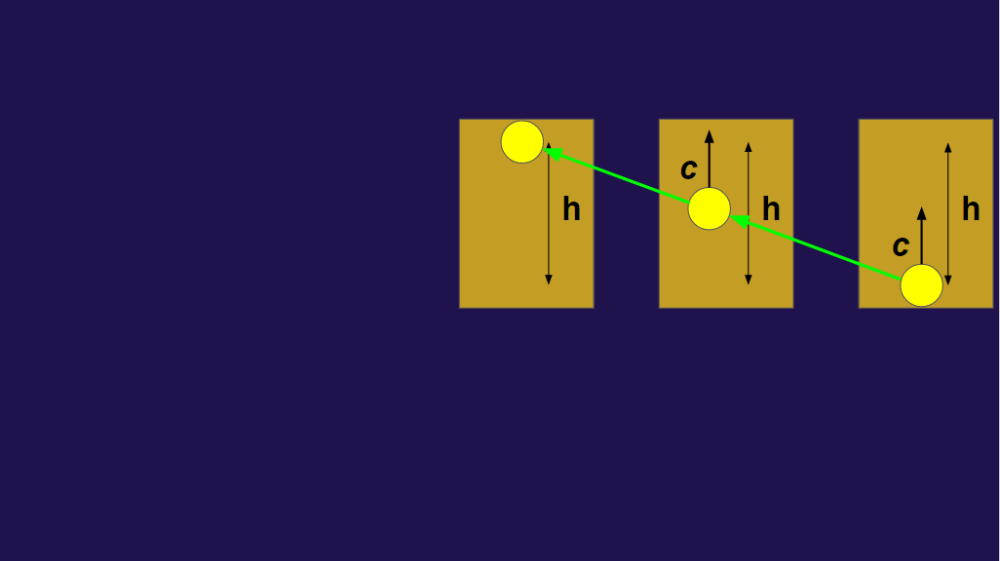
Figure 3: The particle of light’s motion according to person a
(**Note: If the concept illustrated in Figure 3 is confusing, be sure to check out this post**)
So, person a sees the particle of light traveling along the green arrows in Figure 3. We can create a right triangle using the green arrows as the hypotenuse:

Figure 4: A very important triangle
Figure 4 claims that the hypotenuse of the triangle is of length c(ta). In this case, ta is the amount of time it takes for the particle of light to reach the top of the box according to person a (recall that speed, c, times time, ta, is distance). Additionally, one of the legs of the triangle is h and the other leg is La, or the horizontal distance traveled by the particle of light according to person a. Using the Pythagorean theorem, we can relate the aforementioned quantities as follows:

Let’s now imagine that there is another rocket ship passing the box. This rocket ship is traveling at a certain speed, vb, and contains a person, person b. We will say that vb is greater than va (meaning that person b’s rocket ship is traveling faster than person a’s rocket ship):

Figure 5: Person b traveling past the box
As was the case for person a, person b will see the particle of light traveling diagonally as he passes it:

Figure 6: The particle of light’s motion according to person b
And, finally, we can use the green arrows in Figure 6 as the hypotenuse for a right triangle:

Figure 7: Another very important triangle
Although the triangle in Figure 7 is very similar to the triangle in Figure 4, there are a few important things to note. First of all, the hypotenuse of the triangle in Figure 7 is c(tb), where tb is the amount of time it takes for the particle of light to reach the top of the box according to person b. It is important that we establish that ta and tb are not necessarily the same — if va and vb are different, the time dilation that is “influencing” the particle of light will be different for person a and person b (see the equation for the relativistic factor). Furthermore, one of the legs of the triangle is Lb, or the horizontal distance traveled by the particle of light according to person b. Because of length contraction, La and Lb are also not necessarily the same.
What about the other leg of the triangle, h? Recall when we were first discussing length contraction how we saw a ruler “shrink” based on the motion of the observer. This is illustrated by the difference between the ruler in Figure 4 and the ruler in Figure 5 in this post. Notice how the division between the tick marks are smaller in Figure 5’s ruler than they are in Figure 4’s ruler. Also notice that the heights of the rulers in the figures are the same. This is a very important concept: length only contracts in the direction of motion of the observer. So what? Well, in our current situation, the horizontal distance traveled by the particle of light will be contracted because the rocket ships are moving horizontally (which is why La and Lb are not the same). However, the rocket ships are not moving vertically, therefore the vertical distance traveled by the particle of light, h, will not be contracted at all. This means that person a and person b will measure the same value for h.
Let’s use the triangle in Figure 7 to write an equation for h (once again making use of the Pythagorean theorem):

Let’s also rearrange Equation 1 to be in terms of h:

Because both person a’s h and person b’s h are the same, we can combine Equation 3 and Equation 4 and write the following:

Let’s square both sides of Equation 5:

And there we have it! What do we have? Well, let’s think about what Equation 6 is saying: if we take the speed of light and multiply it by the amount of time it takes for the particle of light to reach the top of the rocket ship according to person a, square that quantity, and add the horizontal distance the particle of light travels according to person a squared we get the same value as if we were to take the speed of light and multiply it by the amount of time it takes for the particle of light to reach the top of the rocket according to person b, square that quantity, and add the horizontal distance the particle of light travels according to person b squared (talk about a long sentence!). Remember that we started with person a moving at va and person b moving at vb. va and vb are just variables that we can set to be any value that we want (for example, va = 5 m/s and vb = 10 m/s or va = 0.5c and vb = 0.9c). This means that Equation 6 holds true for any values of va and vb. In other words, no matter what speed person a and person b are moving at, Equation 6 still holds. It must be emphasized that ta and tb are not the same and La and Lb are not the same. Nonetheless, Equation 6 will always be true.
Always be true? That sounds a lot like a value that is absolute. And this is exactly true, in our situation the value
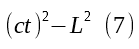
will always be the same, regardless of who the values of t (time) and L (horizontal distance) are measured by. Each and every observer of the particle of light moving in the box, regardless of his speed, will calculate the same value for Expression 7.
So we have found an absolute quantity for this random box situation, but what about other situations? We will soon see that Expression 7 is very important and applies to many other situations. That’s for next week, though! See you then!
If you would prefer a video of the math performed in this post, be sure to check out: https://www.youtube.com/watch?v=SVcJnNMo2wA
(featured image: http://wallpapercave.com/wp/u8PEixm.jpg)